Cómo hacer una recta de regresión lineal en Excel

La regresión lineal es un método estadístico que se utiliza con el objetivo de evaluar la relación entre dos variables. Existe la regresión lineal simple y la regresión múltiple.
En este artículo, te enseñaremos a cómo hacer una recta de regresión línea en Excel de forma rápida y sencilla. Podrás aprender ambos métodos para aplicarlos cuando sea necesario.
Índice de contenidos
Regresión lineal simple
Para hacer una regresión lineal simple en Excel, solo tienes que seguir estos pasos:
- Abre un libro en blanco en Excel.
- Ingresa los datos que deseas relacionar usando las columnas.
- Selecciona los datos presionando clic izquierdo sostenido.
- Ve hacia la pestaña “Insertar”.
- Haz clic sobre el icono de “Insertar gráfico de dispersión (X, Y) o burbujas” y escoge el primer modelo.
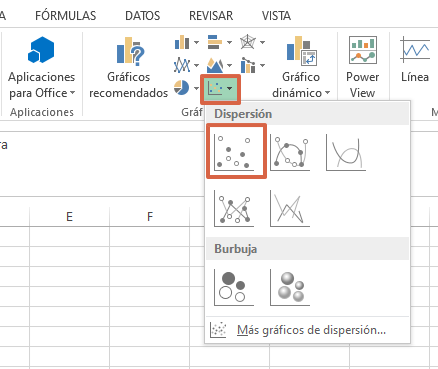
- Observarás que aparecerá una gráfica en Excel. Debes hacer clic derecho sobre los puntos y elegir la opción “Agregar línea de tendencia…”.
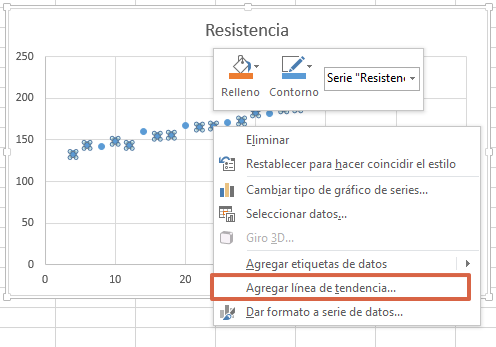
- Elige “Lineal”.
- Desliza las opciones y marca las casillas de “Presentar ecuación en el gráfico” y “Presentar el valor R cuadrado en el gráfico”.
- Ahora, auméntale el tamaño al recuadro en el que aparecerán la ecuación del gráfico y el valor R cuadrado.
Nota: ten en cuenta que la regresión lineal simple se emplea cuando solo cuando vas a analizar dos variables. En caso de que deseas calcular más variables, deberás usar la regresión lineal múltiple.
Regresión lineal múltiple
Si quieres realizar una regresión lineal múltiple en Excel, debes seguir el siguiente procedimiento:
- Abre un libro en blanco en Excel.
- Ahora, presiona “Archivo”.
- Desliza hacia “Opciones”.
- Presiona “Complementos”.
- Haz clic sobre “Ir…”.
- Marca las casillas de “Herramientas para análisis” y “Herramientas para análisis – VBA”. Luego, pulsa “Aceptar”.
- Ve a la pestaña de “Datos”.
- Oprime “Análisis de datos”.
- Busca “Regresión” y pulsa “Aceptar”.
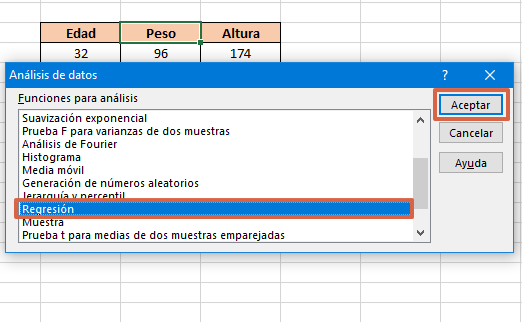
- En “Rango Y de entrada”, selecciona con clic sostenido toda la primera columna de datos que hayas insertado.
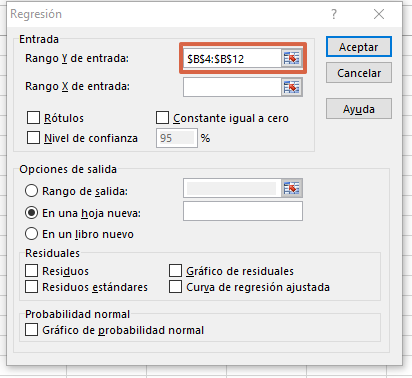
- En “Rango X de entrada”, selecciona con clic sostenido las dos columnas restantes que hayas agregado. Cuando lo hayas hecho, presiona “Aceptar”. Al realizar esta acción, verás que todos los resultados aparecerán en una nueva hoja.
Como has podido detallar, el proceso para hacer una recta de regresión lineal en Excel es bastante sencillo.